dronperminov

29 апреля 2025 в 17:15

Как создать игру 2048 с нуля на чистом Javascript и Canvas

web development, javascript, canvas

Игра 2048 – культовая браузерная головоломка, покорившая интернет своей простотой, увлекательным геймплеем и невероятно лаконичной реализацией. В этой статье мы шаг за шагом создадим собственную версию 2048 с нуля – на чистом Javascript, без единой библиотеки, используя Canvas API для отрисовки.

В процессе вы научитесь:

эффективно работать с массивами и реализовывать механику объединения блоков,
рисовать интерфейс и игровое поле с помощью Canvas API,
обрабатывать нажатия клавиш и динамически управлять состоянием игры.

Этот проект подойдёт как начинающим, так и более опытным разработчикам. Он поможет углубиться в механику рендеринга на Canvas, управление игровым состоянием и взаимодействие с пользователем. В результате вы получите полностью рабочую игру 2048, написанную с нуля своими руками – отличную демонстрацию практических навыков в JavaScript.

Готовы? Поехали!

Подготовка

Первым делом создадим html заготовку: добавим canvas, подключим game2048.js скрипт и создадим объект класса с нашей игрой:

Файл game2048.html

<!DOCTYPE html>
<html>
<head>
    <meta charset="utf-8">
    <meta name="viewport" content="width=device-width, initial-scale=1">
    <title>Игра 2048</title>
</head>
<body>
    <canvas id="canvas"></canvas>

    <script type="text/javascript" src="game2048.js"></script>
    <script>
        const config = {
            canvas: document.getElementById("canvas"),
            n: 4, // размер поля 4x4
            cellSize: 100, // размер ячеек в пикселях
            border: 6, // толщина стенок между ячейками
            scoreHeight: 75 // высота области для отрисовки текущего счёта
        }

        const game = new Game2048(config) // создаём экземпляр класса с игрой
    </script>
</body>
</html>

Для простоты отрисовки наша игра будет выглядеть следующим образом: в верхней части холста по центру будет отрисовываться текущий счёт, а ниже будет квадратное поле из nxn ячеек. Для начала запомним переданные параметры в конфигурации внутри класса:

Файл game2048.js

class Game2048 {
    constructor(config) {
        this.n = config.n ?? 4 // размер поля
        this.cellSize = config.cellSize ?? 100 // размер ячеек в пикселях
        this.scoreHeight = config.scoreHeight ?? 75 // размер области для отрисовки счёта
        this.border = config.border ?? 5 // толщина стенок
        this.fieldSize = this.n * (this.cellSize + this.border) + this.border // размер поля в пикселях

        // ширина холста совпадает с размером поля, а высота складывается из размера поля и области со счётом
        this.canvas = config.canvas
        this.canvas.width = this.fieldSize
        this.canvas.height = this.scoreHeight + this.fieldSize

        // цвета различных игровых объектов
        this.colors = {
            score: "#bdaca0",
            field: "#bdaca0",
            gameOver: "#eee4caba",
            cells: [
                "#cdc2b3", "#efe5da", "#ece0c8", "#f0b17d", "#f19867",
                "#f07e63", "#f46141", "#eacf78", "#edcd66", "#ecc75b",
                "#e8c256", "#e9be4c", "#fd3f3f", "#fe2222", "#000000"
            ]
        }

        this.score = 0 // текущий счёт
    }
}

Создание поля

Хотя игровое поле логически двумерное, мы будем хранить его в одномерном массиве field – это упростит реализацию сдвигов и других операций. При необходимости координаты (i, j) можно превратить в индекс с помощью формулы: index = i * n + j, где n – размер игрового поля:

i \ j |  0    1    2    3
------+----+----+----+----+
   0  |  0 |  1 |  2 |  3 |
      +----+----+----+----+
   1  |  4 |  5 |  6 |  7 |
      +----+----+----+----+
   2  |  8 |  9 | 10 | 11 |
      +----+----+----+----+
   3  | 12 | 13 | 14 | 15 |
      +----+----+----+----+

Значениями массива будут степени двойки, причём пустые ячейки будут иметь нулевое значение. Таким образом изначально все клетки поля будут иметь нулевое значение. Для создания такого массива воспользуемся методом fill с нулевым значением:

Создание игрового поля

constructor(config) {
    ...
    this.field = new Array(this.n * this.n).fill(0) // создаём пустое поле
}

Отрисовка игрового состояния

Чтобы воспользоваться графическими примитивами Canvas API, необходимо получить так называемый графический контекст у холста с помощью метода getContext("2d"). Всю отрисовку будем производить в методе draw, в которм нам необходимо сделать следующее:

очистить canvas с помощью метода ctx.clearRect,
нарисовать текущий счёт с помощью вызова ctx.fillText в методе drawScore,
нарисовать поле и ячейки с помощью вызовов ctx.fillRect в методе drawBoard.

Отрисовка состояния игры

constructor(config) {
    ...
    this.ctx = this.canvas.getContext("2d")

    this.field = new Array(this.n * this.n).fill(0)

    this.draw() // отрисовываем поле
}

// отрисовка состояния игры
draw() {
    this.ctx.clearRect(0, 0, this.canvas.width, this.canvas.height) // очищаем холст

    this.drawScore() // рисуем текущий счёт
    this.drawBoard() // рисуем игровое поле
}

// отрисовка текущего счёта по центру отведённой области
drawScore() {
    this.ctx.textAlign = "center"
    this.ctx.textBaseline = "middle"
    this.ctx.font = `${this.cellSize / 2}px Arial`
    this.ctx.fillStyle = this.colors.score
    this.ctx.fillText(`Score: ${this.score}`, this.fieldSize / 2, this.scoreHeight / 2)
}

// отрисовка поля
drawBoard() {
    // рисуем прямоугольник с цветом поля
    this.ctx.fillStyle = this.colors.field
    this.ctx.fillRect(0, this.scoreHeight, this.fieldSize, this.fieldSize)

    // отрисовываем каждую ячейку поля
    for (let i = 0; i < this.n; i++)
        for (let j = 0; j < this.n; j++)
            this.drawCell(i, j)
}

// отрисовка одной ячейки
drawCell(i, j) {
    const value = this.field[i * this.n + j]
    const x = this.border + j * (this.cellSize + this.border)
    const y = this.scoreHeight + this.border + i * (this.cellSize + this.border)

    // закрашиваем прямоугольик цветом выбранной ячейки
    this.ctx.fillStyle = this.colors.cells[Math.min(value, this.colors.cells.length - 1)]
    this.ctx.fillRect(x, y, this.cellSize, this.cellSize)

    if (value === 0)
        return // не рисуем текст пустой ячейки

    // в центре ячейки выводим текст с её значением
    this.ctx.textAlign = "center"
    this.ctx.textBaseline = "middle"
    this.ctx.font = `${this.cellSize / 2.75}px Arial`
    this.ctx.fillStyle = value < 3 ? this.colors.field : "#ffffff"
    this.ctx.fillText(1 << value, x + this.cellSize / 2, y + this.cellSize / 2)
}

В результате при создании игрового объекта canvas будет выглядеть следующим образом:

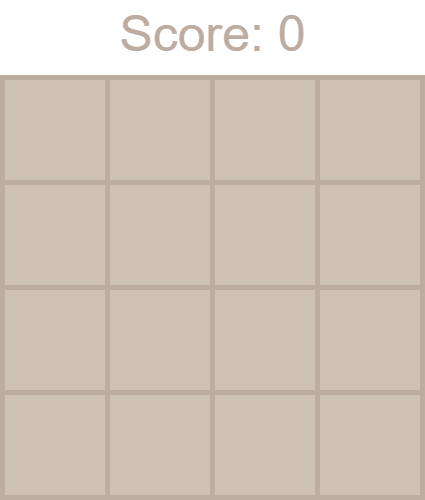
Добавление новых плиток

Теперь, когда мы научились отрисовывать состояние игры, пришло время разобраться с добавлением новых плиток. В игре они добавляются в случайные места, ещё не занятые другими плитками. Для реализации этого нам нужно сформировать индексы пустых ячеек и выбрать из них случайный. Реализуем эту логику с помощью двух методов:

getAvailableCells() – будет возвращать список индексов, значение игрового поля в которых равно нулю,
add(value) – будет выбирать случайное место среди доступных и помещать в него переданное значение плитки:

Добавление плиток

// получение индексов пустых ячеек
getAvailableCells() {
    let available = []

    for (let index = 0; index < this.field.length; index++)
        if (this.field[index] == 0)
            available.push(index)

    return available
}

// добавление плитки со значением value в одну из пустых ячеек
add(value) {
    const availableCells = this.getAvailableCells()
    if (availableCells.length == 0)
        return // если некуда добавлять, то и не добавляем

    // выбираем случайный индекс и помещаем в эту точку на поле переданную плитку
    const index = availableCells[Math.floor(Math.random() * availableCells.length)]
    this.field[index] = value
}

Изначально игра начинается с двух плиток: 2 и 2 или 2 и 4. Первая плитка всегда является двойкой, а вот вторую с 75 процентной вероятностью мы будем делать двойкой, а в 25% случаев четвёркой. Для этого добавим вызов только что написанного метода в конструктор сразу после создания игрового поля:

Добавляем две начальные плитки

constructor(config) {
    ...
    this.field = new Array(this.n * this.n).fill(0)

    // добавляем две начальных плитки в случайные места
    this.add(1)
    this.add(Math.random() < 0.75 ? 1 : 2)

    this.draw()
}

Теперь на поле есть две плитки:

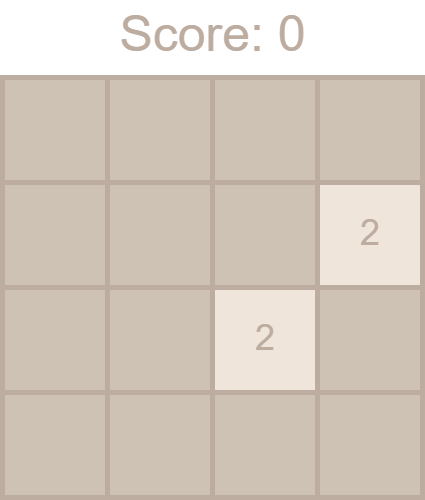
Сдвиг плиток

Пришло время разобраться с самым главным алгоритмом, заложенном в игру 2048: сдвиг плиток в сторону. Рассмотрим, как реализовать сдвиг плиток для группы плиток (в качестве группы будет выступать строка или столбец на поле). Для удобства будем считать, что у нас есть массив индексов с плитками, которые нужно сдвинуть, и метод shift(indices), который будет осуществлять сдвиг и возвращать булево значение – был ли вообще сдвиг. В таком случае для сдвига в одну сторону всего поля, достаточно будет лишь сформировать n списков соответствующих индексов и вызвать метод shift для них.

Алгоритм сдвига плиток без слияния

Для начала будем считать, что нам нужно всего лишь выполнить сдвиг всех плиток в начало кроме пустых (пока что мы сознательно пропускаем случай слияния значений). Для этого мы заведём индекс i = 0, в котором будем хранить положение ячейки, в которую можно поместить непустую плитку. Затем, проходя в цикле по переданным индексам, будем помещать ненулевое значение в позицию с индексом i. Тогда в конце цикла значение i будет соответствовать количество сдвинутых (не пустых) плиток, но в массиве (если были пустые плитки) останутся мусорные значения, которые необходимо занулить (собственно выполнить перенос пустых плиток в конец). Реализуем эту версию в методе shift и затем рассмотрим подробнее принцип её работы:

Алгоритм сдвига плиток без слияния

shift(indices) {
    let i = 0 // индекс очередной позиции

    for (const index of indices)
        if (this.field[index] > 0) // если плитка не пустая
            this.field[indices[i++]] = this.field[index] // помещаем её в новую позицию

    // сдвигаем пустые плитки в конец
    while (i < indices.length)
        this.field[indices[i++]] = 0
}

Предположим, что мы сдвигаем элементы с индексами [0, 1, 2, 3] со значениями [0, 7, 0, 5]. Рассмотрим, что делает алгоритм по шагам:

Шаг 1. i = 0, index = 0: значение на поле равно 0, поэтому пропускаем его и идём дальше;
Шаг 2. i = 0, index = 1: значение на поле равно 7, записываем его по индексу indices[i++] = 0, а значения становятся такими: [7, 7, 0, 5];
Шаг 3. i = 1, index = 2: значение на поле равно 0, пропускаем его и идём дальше
Шаг 4. i = 1, index = 3: значение на поле равно 5, записываем его по индексу indices[i++] = 1, а значения становятся такими: [7, 5, 0, 5];
Шаг 5. i = 2, дозаписываем оставшуюся часть массива нулями: [7, 5, 0, 0]

В результате мы действительно осуществили сдвиг непустых плиток в начало, а значит пришло время рассмотреть случай со слиянием.

Полноценный алгоритм сдвига плиток

Версия, учитывающая слияние, на самом деле будет не сильно отличаться от уже написанной. В момент перемещения очередной плитки нам нужно понять, не совпадает ли её значение со значением предыдущей непустой плитки. В том случае, если значения совпадают, то вместо сдвига позиции по i, необходимо увеличить значение предыдущей ячейки на 1 (а также увеличить счёт на величину полученной плитки). При этом необходимо учесть, что сразу после слияния нам нельзя выполнять новое слияние со следующей плиткой, даже если её значение совпадает с только что увеличенным (случай [3, 3, 4, 5] должен превратиться в [4, 4, 5, 0], а не в [6, 0, 0, 0] в рамках одного сдвига). Обновим наш метод:

Алгоритм сдвига плиток

shift(indices) {
    let i = 0
    let merge = false // было ли перед этим слияние

    for (const index of indices) {
        if (this.field[index] == 0)
            continue // пустые ячейки пропускаем

        // можем выполнить слияние, если значения совпадают и перед этим не было слияния
        merge = !merge && i > 0 && this.field[indices[i - 1]] == this.field[index]

        if (merge) {
            this.field[indices[i - 1]]++ // удваиваем значение предыдущей плитки
            this.score += 1 << (this.field[index] + 1) // увеличиваем счёт
        }
        else
            this.field[indices[i++]] = this.field[index] // просто сдвигаем ячейку
    }

    while (i < indices.length)
        this.field[indices[i++]] = 0
}

Теперь остаётся только вернуть флаг наличия сдвига: сдвиг был, если было хоть одно слияние или же непустая плитка перемещалась на новое место:

Добавляем флаг наличия сдвига

shift(indices) {
    let shifted = false // был ли сдвиг

    for (const index of indices) {
        ...
        merge = ...

        // сдвиг был, если было слияние или плитка перемещалась на новое место
        shifted |= merge || indices[i] != index
    }

    ...
    return shifted
}

Сдвигаем плитки в одну сторону

Теперь у нас есть метод, позволяющий сдвинуть один набор плиток, а нам нужно сдвинуть сразу n таких наборов. Мы, конечно, могли бы написать методы shiftLeft, shiftRight, shiftUp и shiftDown, продублировав кучу кода, но мы пойдём другим путём. Рассмотрим, как выглядели бы методы сдвига всех строк влево и вверх:

Сдвиги влево и вверх

shiftLeft() {
    let shifted = false

    for (let row = 0; row < this.n; row++) {
        let indices = []

        // формируем список индексов для каждой строки
        for (let column = 0; column < this.n; column++)
            indices.push(row * this.n + column)

        shift |= this.shift(indices) // выполняем сдвиг строки
    }

    return shifted
}

shiftUp() {
    let shifted = false

    for (let column = 0; column < this.n; column++) {
        let indices = []

        // формируем список индексов для каждого столбца
        for (let row = 0; row < this.n; row++)
            indices.push(row + column * this.n)

        shift |= this.shift(indices) // выполняем сдвиг столбца
    }

    return shifted
}

Как видите, методы очень сильно похожи друг на друга. Мы можем выделить общую часть и реализовать метод shiftCells, принимающий определённые параметры так, чтобы его можно было использовать для всех четырёх сторон сразу:

Сдвиг ячеек в произвольную сторону

shiftCells(/* какие-то параметры*/) {
    let shifted = false

    for (let i = 0; i < this.n; i++) {
        let indices = []

        // формируем список индексов для каждой группы
        for (let j = 0; j < this.n; j++)
            indices.push(/* какая-то формула с i и j*/)

        shift |= this.shift(indices) // выполняем сдвиг
    }

    return shifted
}

Теперь нам нужно понять, как должна выглядеть формула для заполнения индексов. Мы уже знаем, что для сдвига влево она выглядит как i + j * n, а для сдвига вверх она должна быть i * n + j. Но что на счёт сдвига вправо и вниз?

Рассмотрим сначала сдвиг вправо:

Для строки с индексом 0 мы должны получить элементы с индексами 3, 2, 1 и 0.
Для строки с индексом 1 мы должны получить элементы с индексами 7, 6, 5 и 4.
Для строки с индексом 3 (n - 1) мы должны получить элементы с индексами 15, 14, 13 и 12.

Видно, что с ростом j значение уменьшается на 1, значит в формуле явно будет фигурировать -j. С ростом же переменной i увеличивается начальное значение, причём оно равно в точности i * n + n - 1. Таким образом общая формула заполнения индексов для сдвига вправо будет такой: i * n - j + n - 1.

Рассмотрим теперь сдвиг вниз:

Для столбца с индексом 0 мы должны получить элементы с индексами 12, 8, 4 и 0.
Для столбца с индексом 1 мы должны получить элементы с индексами 13, 9, 5 и 1.
Для столбца с индексом 3 (n - 1) мы должны получить элементы с индексами 15, 11, 7 и 3.

Видно, что с увеличением j значение уменьшается в точности на n. А с ростом i значение увеличивается на единицу. Остаётся лишь найти начальное значение, которое вычисляется как n * (n - 1), а итоговая формула будет иметь вид i - j * n + n * (n - 1).

Легко заметить, что все 4 формулы можно легко представить в виде di * i + dj * j + d. А значит наш метод будет переписан следующим образом:

Сдвиг ячеек в произвольную сторону

shiftCells(di, dj, d) {
    let shifted = false

    for (let i = 0; i < this.n; i++) {
        // используем методы массива для более элегантного создания массива индексов
        const indices = Array.from(Array(this.n), (_, j) => i * di + j * dj + d)
        shifted |= this.shift(indices)
    }

    return shifted
}

Обрабатываем клавиатуру

Для непосредственно игры нам теперь очень сильно не хватает управления с клавиатуры. Для этого навесим обработчик keyDown на документ (document), внутри которого будем выполнять сдвиги в разные стороны в зависимости от нажатой клавиши. Если была нажата одна из стрелок, то добавим новую плитку и обновим состояние игрового поля:

Обработка нажатий клавиш клавиатуры

constructor(config) {
    ...
    document.addEventListener("keydown", e => this.keyDown(e))
}

keyDown(e) {
    let shifted = false

    if (e.key == "ArrowLeft")
        shifted = this.shiftCells(this.n, 1, 0)
    else if (e.key == "ArrowRight")
        shifted = this.shiftCells(this.n, -1, this.n - 1)
    else if (e.key == "ArrowUp")
        shifted = this.shiftCells(1, this.n, 0)
    else if (e.key == "ArrowDown")
        shifted = this.shiftCells(1, -this.n, (this.n - 1) * this.n)

    // если ничего не сдинули, то и делать ничего не будем
    if (!shifted)
        return

    // добавляем новую плитку и перерисовываем поле
    this.add(Math.random() < 0.75 ? 1 : 2)
    this.draw()
}

Теперь игрой можно управлять с помощью стрелок: плитки будут сдвигаться и сливаться, а счёт будет постепенно расти.

У всего есть конец

К этому моменту у нас есть работающая игра 2048, которая позволяет управлять ей бесконечно долго, однако в какой-то момент сдвигать плитки станет просто некуда и именно тогда нам необходимо отрисовать экран с завершающей фразой "Game over!". Но прежде чем переходить к отрисовке, давайте разберёмся, а как собственно понять, что сдвигать плитки больше некуда?

В качестве простого (но неверного) решения можно было бы запустить shiftCells для всех 4 направлений и проверить их результат. Но в таком случае нужно было бы сохранять состояние поля и восстанавливать его после, если сдвиг был. Поэтому так мы делать точно не будем.

На самом деле сдвиг можно сделать в двух случаях:

есть хотя бы одна пустая ячейка;
по горизонтали или по вертикали есть две плитки с одинаковым значением.

Для удобства реализуем метод canShift, проверяющий эти условия:

Проверка осуществимости сдвига

canShift() {
    // если есть хотя бы одна свободная клетка, то сдвиг возможен
    if (this.getAvailableCells().length > 0)
        return true

    // свободных клеток нет, так что нужно проверить все соседние ячейки
    for (let i = 0; i < this.n; i++)
        for (let j = 1; j < this.n; j++)
            if (this.field[i * this.n + j] == this.field[i * this.n + (j - 1)] || this.field[j * this.n + i] == this.field[(j - 1) * this.n + i])
                return true

    return false
}

Теперь добавим метод drawGameOver, выполняющий отрисовку окончания игры. Чтобы сильно ничего не менять, добавим в класс флаг gameOver, а внутри draw будем отрисовывать финальный экран, если этот флаг установлен:

Отрисовка конца игры

constructor(config) {
    ...
    this.gameOver = false // флаг окончания игры
}

draw() {
    this.ctx.clearRect(0, 0, this.canvas.width, this.canvas.height)

    this.drawScore()
    this.drawBoard()

    if (this.isGameOver)
        this.drawGameOver()
}

drawGameOver() {
    this.ctx.fillStyle = this.colors.gameOver
    this.ctx.fillRect(0, this.scoreHeight, this.fieldSize, this.fieldSize)
    this.ctx.fillStyle = "#ffffff"
    this.ctx.font = `${this.cellSize / 1.5}px Arial`
    this.ctx.fillText("Game over!", this.fieldSize / 2, this.scoreHeight + this.fieldSize / 2)
}

Теперь внутри обработчика keyDown остаётся только обновить значение флага и можно считать игру завершённой:

Обработка конца игры

keyDown(e) {
    // ели игра окончена, то больше не обрабатываем клавиши
    if (this.gameOver)
        return

    ...

    this.add(Math.random() < 0.75 ? 1 : 2)
    this.gameOver = !this.canShift() // обновляем флаг окончания игры
    this.draw()
}

Теперь в конце игры будет понятно, что больше сдвигать некуда и необходимо начать заново.

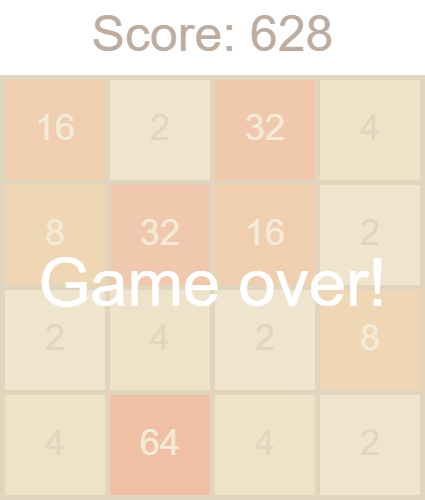
Заключение

Поздравляю! Спустя всего 180 строк javascript кода у нас есть минималистичный, но полностью рабочий клон культовой игры 2048, а также целый багаж знаний по работе с Canvas API и некоторыми методами работы с массивами.

Конечно, в этой версии много изъянов: она не поддерживает touch события, в ней нет плавных анимаций переходов и, если закрыть вкладку, то прогресс будет утерян. Всё это можно запросто добавить в текущую версию буквально в ещё несколько js строк, однако это выходит за рамки данного гайда.

Если вы дочитали эту статью до конца и запустили свою игру – поздравляю! Вы только что собрали свою версию 2048 с нуля. Играйте, улучшайте и не бойтесь экспериментировать.

Итоговый файл game2048.html (остался без изменений)

    <!DOCTYPE html>
<html>
<head>
    <meta charset="utf-8">
    <meta name="viewport" content="width=device-width, initial-scale=1">
    <title>Игра 2048</title>
</head>
<body>
    <canvas id="canvas"></canvas>

    <script type="text/javascript" src="game2048.js"></script>
    <script>
        const config = {
            canvas: document.getElementById("canvas"),
            n: 4, // размер поля 4x4
            cellSize: 100, // размер ячеек в пикселях
            border: 6, // толщина стенок между ячейками
            scoreHeight: 75 // высота области для отрисовки текущего счёта
        }

        const game = new Game2048(config) // создаём экземпляр класса с игрой
    </script>
</body>
</html>

Итоговый файл game2048.js

class Game2048 {
    constructor(config) {
        this.n = config.n ?? 4
        this.cellSize = config.cellSize ?? 100
        this.scoreHeight = config.scoreHeight ?? 75
        this.border = config.border ?? 5
        this.fieldSize = this.n * (this.cellSize + this.border) + this.border

        this.canvas = config.canvas
        this.canvas.width = this.fieldSize
        this.canvas.height = this.scoreHeight + this.fieldSize

        this.ctx = this.canvas.getContext("2d")

        this.colors = {
            score: "#bdaca0",
            field: "#bdaca0",
            gameOver: "#eee4caba",
            cells: [
                "#cdc2b3", "#efe5da", "#ece0c8", "#f0b17d", "#f19867",
                "#f07e63", "#f46141", "#eacf78", "#edcd66", "#ecc75b",
                "#e8c256", "#e9be4c", "#fd3f3f", "#fe2222", "#000000"
            ]
        }

        this.field = new Array(this.n * this.n).fill(0)
        this.score = 0
        this.gameOver = false

        this.add(1)
        this.add(Math.random() < 0.75 ? 1 : 2)
        this.draw()

        document.addEventListener("keydown", e => this.keyDown(e))
    }

    getAvailableCells() {
        let available = []

        for (let index = 0; index < this.field.length; index++)
            if (this.field[index] == 0)
                available.push(index)

        return available
    }

    add(value) {
        const availableCells = this.getAvailableCells()
        if (availableCells.length == 0)
            return

        const index = availableCells[Math.floor(Math.random() * availableCells.length)]
        this.field[index] = value
    }

    draw() {
        this.ctx.clearRect(0, 0, this.canvas.width, this.canvas.height)

        this.drawScore()
        this.drawBoard()

        if (this.gameOver)
            this.drawGameOver()
    }

    drawScore() {
        this.ctx.textAlign = "center"
        this.ctx.textBaseline = "middle"
        this.ctx.font = `${this.cellSize / 2}px Arial`
        this.ctx.fillStyle = this.colors.score
        this.ctx.fillText(`Score: ${this.score}`, this.fieldSize / 2, this.scoreHeight / 2)
    }

    drawBoard() {
        this.ctx.fillStyle = this.colors.field
        this.ctx.fillRect(0, this.scoreHeight, this.fieldSize, this.fieldSize)

        for (let i = 0; i < this.n; i++)
            for (let j = 0; j < this.n; j++)
                this.drawCell(i, j)
    }

    drawCell(i, j) {
        const value = this.field[i * this.n + j]
        const x = this.border + j * (this.cellSize + this.border)
        const y = this.scoreHeight + this.border + i * (this.cellSize + this.border)

        this.ctx.fillStyle = this.colors.cells[Math.min(value, this.colors.cells.length - 1)]
        this.ctx.fillRect(x, y, this.cellSize, this.cellSize)

        if (value === 0)
            return

        this.ctx.font = `${this.cellSize / 2.75}px Arial`
        this.ctx.fillStyle = value < 3 ? this.colors.field : "#ffffff"
        this.ctx.fillText(1 << value, x + this.cellSize / 2, y + this.cellSize / 2)
    }

    drawGameOver() {
        this.ctx.fillStyle = this.colors.gameOver
        this.ctx.fillRect(0, this.scoreHeight, this.fieldSize, this.fieldSize)
        this.ctx.fillStyle = "#ffffff"
        this.ctx.font = `${this.cellSize / 1.5}px Arial`
        this.ctx.fillText("Game over!", this.fieldSize / 2, this.scoreHeight + this.fieldSize / 2)
    }

    canShift() {
        if (this.getAvailableCells().length > 0)
            return true

        for (let i = 0; i < this.n; i++)
            for (let j = 1; j < this.n; j++)
                if (this.field[i * this.n + j] == this.field[i * this.n + (j - 1)] || this.field[j * this.n + i] == this.field[(j - 1) * this.n + i])
                    return true

        return false
    }

    shift(indices) {
        let i = 0
        let merge = false
        let shifted = false

        for (const index of indices) {
            if (this.field[index] == 0)
                continue

            merge = !merge && i > 0 && this.field[indices[i - 1]] == this.field[index]
            shifted |= merge || indices[i] != index

            if (merge) {
                this.field[indices[i - 1]]++
                this.score += 1 << (this.field[index] + 1)
            }
            else
                this.field[indices[i++]] = this.field[index]
        }

        while (i < indices.length)
            this.field[indices[i++]] = 0

        return shifted
    }

    shiftCells(di, dj, d) {
        let shifted = false

        for (let i = 0; i < this.n; i++) {
            const indices = Array.from(Array(this.n), (_, j) => i * di + j * dj + d)
            shifted |= this.shift(indices)
        }

        return shifted
    }

    keyDown(e) {
        if (this.gameOver)
            return

        let shifted = false

        if (e.key == "ArrowLeft")
            shifted = this.shiftCells(this.n, 1, 0)
        else if (e.key == "ArrowRight")
            shifted = this.shiftCells(this.n, -1, this.n - 1)
        else if (e.key == "ArrowUp")
            shifted = this.shiftCells(1, this.n, 0)
        else if (e.key == "ArrowDown")
            shifted = this.shiftCells(1, -this.n, (this.n - 1) * this.n)

        if (!shifted)
            return

        this.add(Math.random() < 0.75 ? 1 : 2)
        this.gameOver = !this.canShift()
        this.draw()
    }
}